¿Qué son los números índice?
El número índice es una medida estadística diseñada para poner de relieve cambios en una variable o en un grupo de variables relacionadas con respecto al tiempo, situación geográfica, ingreso o cualquier otra característica.
Este tipo de número puede definirse también como un valor relativo con base igual a 100% o un múltiplo de 100% tal como 10 y 100, que permite medir qué tanto una variable ha cambiado con el tiempo.
Calculamos un número índice encontrando el cociente del valor actual entre un valor base. Luego multiplicamos el número resultante por 100, para expresar el índice como un porcentaje. Este valor final es el porcentaje relativo. El número índice para el punto base en el tiempo siempre es 100.
¿Para qué sirven?
Los números índices son útiles cuando se quiere comparar variables o magnitudes que están medidas en unidades distintas. Por ejemplo, con los números índices podemos comparar los costes de alimentación o de otros servicios en una ciudad durante un año con los del año anterior, o la producción de arroz en un año en una zona del país con la otra zona.
Aunque se usa principalmente en Economía e Industria, los números índices son aplicables en muchos campos. En Educación, por ejemplo, se pueden usar los números índices para comparar la inteligencia relativa de estudiantes en sitios diferentes o en años diferentes.
Muchos gobiernos se ocupan de elaborar números índice con el propósito de predecir condiciones económicas o industriales, tales como: índices de precios, de producción, salariales, del consumidor, poder adquisitivo, costo de vida, etc.
En la administración se utilizan como parte de un cálculo intermedio para entender mejor otra información.
Clasificación de los números índice
Los números índice se clasifican en:- Simples
- Compuestos, estos a su vez se clasifican en: Sin ponderar,ponderados.
Índices Simples:
Son los que se refieren a una sola magnitud o concepto, y, por tanto, nos proporcionan la variación que ha sufrido esa magnitud en dos períodos distintos. La forma usual de expresar un índice simple es:
I = mt X 100
mo
donde mt es la magnitud en el período t, y mo es la magnitud en el período-base.
Índices Compuestos
Si lo que deseamos es medir la evolución en el tiempo de una magnitud compleja, o conjunto de magnitudes simples, como, por ejemplo, el precio de las frutas, en este caso no se podrá utilizar un índice simple, ya que tendríamos diferentes precios para cada una de las variedades que presenta este tipo de alimentos (naranjas, manzanas, peras, etc).
En estos casos, hemos de acudir a otro tipo de índices, denominados en la literatura índices compuestos, que se obtienen por combinación de los índices simples de cada una de las magnitudes que estamos analizando.
Existen diferentes formas o criterios para obtener el índice compuesto. Una primera clasificación consiste en distinguir entre índices compuestos sin ponderar e índices compuestos ponderados.
Índices Compuestos Sin Ponderar:
Son los que tratan de medir la evolución de una magnitud compleja, pero donde las diferentes magnitudes simples que intervienen tienen todas la misma importancia.
5.2.2 Índices Compuestos Ponderados
Aunque los índices compuestos ponderados se pueden obtener para todo tipo de variables, los más importantes son los que miden las variaciones en los precios.
El índice de precios: compara niveles de precios de un período a otro. El índice de precios al consumidor (IPC) mide los cambios globales de precios de una variedad de bienes de consumo y de servicios, y se le utiliza para definir el costo de vida.
El índice de cantidad: mide qué tanto cambia el número o la cantidad de una variable en el tiempo.
El índice de valor: mide los cambios en el valor monetario total; es decir, mide los cambios en el valor en pesos de una variable, combina los cambios en precio y cantidad para presentar un índice con más información.
Aplicaciones de los Números índice
Las relaciones de precios es uno de los ejemplos más simple de un número índice, que no es sino el cociente entre el precio de un artículo en un período determinado y su precio en otro período, conocido como período base o período de referencia. Suponiendo que los precios en cada período son constantes. Si no lo son, podemos tomar un promedio adecuado para el período de modo que la suposición sea esencialmente válida.
La fórmula para calcular un índice de precios es la siguiente:
Relaciones de precios= ——— X 100
Po
En donde:
Pn= es el período dado.
Po= es el período base.
La relación de precios se expresa habitualmente como un porcentaje multiplicándola por 100.
En general, si Pa y Pb son los precios de un artículo durante los períodos a y b, respectivamente, la relación de precios en el período b con respecto al período a se define como Pb/Pa y se denota por Pa/b’, notación que facilita el entendimiento; con esta notación la relación de precios en la ecuación:
Pn
Rp= —— , se denota por Po/n.Po
Ejemplo:
Supongamos que los precios pagados a pescadores por el lenguado fueron en los años 1990 y 1991 de Bs. 120 y 100 respectivamente, siendo 1990 el año base y 1991 el año dado.
Al seleccionar el período base para un índice en particular se deben observar dos reglas: Primera; el período seleccionado debe ser, en cuanto sea posible, de normalidad o estabilidad económica, no en uno que se encuentre o en el punto máximo de una economía en expansión, cerca de él, o en la sima de una recesión o economía en declinación. Así, por ejemplo, los años de la depresión de la década de 1930 no puede utilizarse como años base, ya que durante este período se produjo una reducción brusca en los precios, el año base debe ser un año en el que la actividad económica transcurra sin estas bruscas fluctuaciones. Segunda: el período base debe ser reciente, para que las comparaciones no resulten afectadas indebidamente por cambios en tecnología, calidad del producto o cambios de actitud frente al mismo, intereses, gustos y hábitos de los consumidores.
para cada valor de renta, la curva de Lorentz puede encontrarse analíticamente en función de esta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:
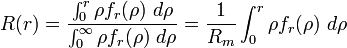
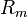es la renta media. Las ecuaciones 1 y 2 constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.
la pendiente será nula (aun en el caso 
el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
con una distribución exponencial la densidad de probabilidad de la distribución será:
de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
.
